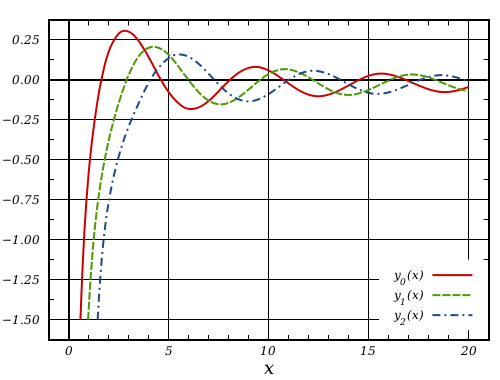
Base on the class taught by Prof. Frabricant.
( 1 − x 2 ) y ′ ′ − 2 x y ′ + l ( l + 1 ) y = 0 , x ∈ [ − 1 , 1 ] [ ( 1 − x 2 ) d 2 d x 2 − 2 x d d x + l ( l + 1 ) ] y = 0 \fbox{$(1-x^2)y''-2xy'+l(l+1)y = 0$},\quad x\in[-1,1]\\
\left[(1-x^2)\dfrac{d^2}{dx^2}-2x\dfrac{d}{dx}+l(l+1)\right]y = 0\\
( 1 − x 2 ) y ′ ′ − 2 x y ′ + l ( l + 1 ) y = 0 , x ∈ [ − 1 , 1 ] [ ( 1 − x 2 ) d x 2 d 2 − 2 x d x d + l ( l + 1 ) ] y = 0
Or, for my conventience to recall the “eigenvalue problem”, I should write the eigenvalue problem of Y ( y ) Y(y) Y ( y )
( 1 − y 2 ) Y ′ ′ Y − 2 y Y ′ Y = − l ( l + 1 ) (1-y^2)\dfrac{Y''}{Y}-2y\dfrac{Y'}{Y} = -l(l+1)
( 1 − y 2 ) Y Y ′ ′ − 2 y Y Y ′ = − l ( l + 1 )
It’s not difficult if you use polynomials(y = a 0 + a 1 x + a 2 x 2 + a 3 x 3 ⋯ y = a_0+a_1x+a_2x^2+a_3x^3\cdots y = a 0 + a 1 x + a 2 x 2 + a 3 x 3 ⋯
a n + 2 = − ( l − n ) ( l + n + 1 ) ( n + 2 ) ( n + 1 ) a n a_{n+2} = -\dfrac{(l-n)(l+n+1)}{(n+2)(n+1)}a_n
a n + 2 = − ( n + 2 ) ( n + 1 ) ( l − n ) ( l + n + 1 ) a n
The Legendre polynomials are:
P 0 ( x ) = 1 P 1 ( x ) = x P 2 ( x ) = 1 2 ( 3 x 2 − 1 ) ⋯ \begin{aligned}
P_0(x) & = 1\\
P_1(x) & = x\\
P_2(x) & = \frac{1}{2}(3x^2-1)\\
\cdots
\end{aligned}
P 0 ( x ) P 1 ( x ) P 2 ( x ) ⋯ = 1 = x = 2 1 ( 3 x 2 − 1 )
Rodrigues’ formula : an easy way to get the Legendre polynomials (the solution of the eigenvalue problem) directly.
P l ( x ) = 1 2 l l ! d l d x l ( x 2 − 1 ) l P_l(x) = \dfrac{1}{2^ll!}\dfrac{d^l}{dx^l}(x^2-1)^l
P l ( x ) = 2 l l ! 1 d x l d l ( x 2 − 1 ) l
In order to proove the Rodrigues’ formula, you only need to plug it into the original ordinary differential equation.
Generating function : A function whose factors of Taylor expansion are Legendre polynomials.
Φ ( x , h ) = ( 1 − 2 x h + h 2 ) − 1 / 2 = P 0 ( x ) + h P 1 ( x ) + h 2 P 2 ( x ) + ⋯ , ∣ h ∣ < 1 \Phi(x,h) = (1-2xh+h^2)^{-1/2} = P_0(x) + hP_1(x)+ h^2P_2(x)+\cdots,\quad |h|<1
Φ ( x , h ) = ( 1 − 2 x h + h 2 ) − 1 / 2 = P 0 ( x ) + h P 1 ( x ) + h 2 P 2 ( x ) + ⋯ , ∣ h ∣ < 1
In order to proove this, we need first know the fact below:
( 1 − x 2 ) ∂ 2 Φ ∂ x 2 − 2 x ∂ Φ ∂ x + h ∂ 2 ∂ h 2 ( h Φ ) = 0 (1-x^2)\dfrac{\partial^2\Phi}{\partial x^2} - 2x\dfrac{\partial\Phi}{\partial x}+h\dfrac{\partial^2}{\partial h^2}(h\Phi) = 0
( 1 − x 2 ) ∂ x 2 ∂ 2 Φ − 2 x ∂ x ∂ Φ + h ∂ h 2 ∂ 2 ( h Φ ) = 0
Recursion Relations (Boas Chapter12 Page 570 )
l P l ( x ) = ( 2 l − 1 ) x P l − 1 ( x ) − ( l − 1 ) P l − 2 ( x ) x P l ′ ( x ) − P l − 1 ′ ( x ) = l P l ( x ) P l ′ ( x ) − x P l − 1 ′ ( x ) = l P l − 1 ( x ) lP_l(x) = (2l-1)xP_{l-1}(x) - (l-1)P_{l-2}(x)\\
xP_l'(x)-P'_{l-1}(x) = lP_l(x)\\
P'_l(x)-xP'_{l-1}(x) = lP_{l-1}(x)\\
l P l ( x ) = ( 2 l − 1 ) x P l − 1 ( x ) − ( l − 1 ) P l − 2 ( x ) x P l ′ ( x ) − P l − 1 ′ ( x ) = l P l ( x ) P l ′ ( x ) − x P l − 1 ′ ( x ) = l P l − 1 ( x )
Parity :
P l ( − x ) = ( − 1 ) l P l ( x ) P_l(-x) = (-1)^lP_l(x)
P l ( − x ) = ( − 1 ) l P l ( x )
Orthogonality :
∫ − 1 1 [ P l ( x ) ] 2 d x = 2 2 l + 1 \int^1_{-1}[P_l(x)]^2dx = \dfrac{2}{2l+1}
∫ − 1 1 [ P l ( x ) ] 2 d x = 2 l + 1 2
( 1 − x 2 ) y ′ ′ − 2 x y + [ l ( l + 1 ) − m 2 1 − x 2 ] y = 0 , x ∈ [ − 1 , 1 ] \fbox{$(1-x^2)y''-2xy + \left[l(l+1)-\dfrac{m^2}{1-x^2}\right]y = 0$},\quad x\in[-1,1]
( 1 − x 2 ) y ′ ′ − 2 x y + [ l ( l + 1 ) − 1 − x 2 m 2 ] y = 0 , x ∈ [ − 1 , 1 ]
Or, in the format of the eigenvalue problem of Y ( y ) Y(y) Y ( y )
( 1 − y 2 ) Y ′ ′ Y − 2 y Y ′ Y − m 2 1 − y 2 = − l ( l + 1 ) (1-y^2)\dfrac{Y''}{Y}-2y\dfrac{Y'}{Y} - \dfrac{m^2}{1-y^2} = -l(l+1)
( 1 − y 2 ) Y Y ′ ′ − 2 y Y Y ′ − 1 − y 2 m 2 = − l ( l + 1 )
For solving the associated legendre function, we first substitute y = ( 1 − x 2 ) m / 2 u y = (1-x^2)^{m/2}u y = ( 1 − x 2 ) m / 2 u m 2 1 − x 2 \dfrac{m^2}{1-x^2} 1 − x 2 m 2 m ( m + 1 ) m(m+1) m ( m + 1 )
( 1 − x 2 ) u ′ ′ − 2 ( m + 1 ) x u ′ + [ l ( l + 1 ) − m ( m + 1 ) ] u = 0 differentiate ⟶ ( 1 − x 2 ) ( u ′ ) ′ ′ − 2 ( m + 2 ) x ( u ′ ) ′ + [ l ( l + 1 ) − ( m + 1 ) ( m + 2 ) ] u ′ = 0 (1-x^2)u''-2(m+1)xu'+[l(l+1)-m(m+1)]u = 0\\
\text{differentiate}\longrightarrow(1-x^2)(u')'' -2(m+2)x(u')'+[l(l+1)-(m+1)(m+2)]u' = 0
( 1 − x 2 ) u ′ ′ − 2 ( m + 1 ) x u ′ + [ l ( l + 1 ) − m ( m + 1 ) ] u = 0 differentiate ⟶ ( 1 − x 2 ) ( u ′ ) ′ ′ − 2 ( m + 2 ) x ( u ′ ) ′ + [ l ( l + 1 ) − ( m + 1 ) ( m + 2 ) ] u ′ = 0
Equation doesn’t change if u → u , m → m + 1 ′ u\rightarrow u, m\rightarrow m+1' u → u , m → m + 1 ′ u = P l u=P_l u = P l m = 0 m=0 m = 0 P l ′ P'_l P l ′ m = 1 m=1 m = 1
u m = d m d x m P l ( x ) P l m ( x ) = y = ( 1 − x 2 ) m / 2 d m d x m P l ( x ) u^m = \dfrac{d^m}{dx^m}P_l(x)\\
P^m_l(x) = y = (1-x^2)^{m/2}\dfrac{d^m}{dx^m}P_l(x)
u m = d x m d m P l ( x ) P l m ( x ) = y = ( 1 − x 2 ) m / 2 d x m d m P l ( x )
In Boas’ book, there’s no ( − 1 ) m (-1)^m ( − 1 ) m P l m ( x ) P^m_l(x) P l m ( x ) P l m ( x ) = ( − 1 ) m ( 1 − x 2 ) m / 2 d m d x m P l ( x ) P^m_l(x) = (-1)^m(1-x^2)^{m/2}\dfrac{d^m}{dx^m}P_l(x) P l m ( x ) = ( − 1 ) m ( 1 − x 2 ) m / 2 d x m d m P l ( x ) Wikipedia: Associated Legendre polynomials
Rodrigues’ formula :
P l m ( x ) = 1 2 l l ! ( 1 − x 2 ) m / 2 d l + m d x l + m ( x 2 − 1 ) l P_l^m(x) = \dfrac{1}{2^ll!}(1-x^2)^{m/2}\dfrac{d^{l+m}}{dx^{l+m}}(x^2-1)^l
P l m ( x ) = 2 l l ! 1 ( 1 − x 2 ) m / 2 d x l + m d l + m ( x 2 − 1 ) l
Parity :
P l m ( − x ) = ( − 1 ) l + m P l m ( x ) P^m_l(-x) = (-1)^{l+m}P_l^m(x)
P l m ( − x ) = ( − 1 ) l + m P l m ( x )
Orthogonality :
∫ − 1 1 [ P l m ( x ) ] 2 d x = 2 2 l + 1 ( l + m ) ! ( l − m ) ! \int^1_{-1}[P^m_l(x)]^2dx = \dfrac{2}{2l+1}\dfrac{(l+m)!}{(l-m)!}
∫ − 1 1 [ P l m ( x ) ] 2 d x = 2 l + 1 2 ( l − m ) ! ( l + m ) !
Negative m m m :
P l − m ( x ) = ( − 1 ) m ( l − m ) ! ( l + m ) ! P l m ( x ) P_l^{-m}(x) = (-1)^m\dfrac{(l-m)!}{(l+m)!}P_l^m(x)
P l − m ( x ) = ( − 1 ) m ( l + m ) ! ( l − m ) ! P l m ( x )
Note that P l m P^m_l P l m P l − m P^{-m}_l P l − m P l m P^m_l P l m ( − 1 ) m (-1)^m ( − 1 ) m
→ \rightarrow →
Wikipedia: Spherical harmonics .( − 1 ) m (-1)^m ( − 1 ) m
Y l m ( θ , ϕ ) = P l m ( cos θ ) e i m ϕ × (normalization factor) (normalization factor) = 2 l + 1 4 π ( l − m ) ! ( l + m ) ! Y^m_l(\theta,\phi) = P_l^m(\cos\theta)e^{im\phi}\times\text{(normalization factor)}\\
\text{(normalization factor)} = \sqrt{\dfrac{2l+1}{4\pi}\dfrac{(l-m)!}{(l+m)!}}
Y l m ( θ , ϕ ) = P l m ( cos θ ) e i m ϕ × (normalization factor) (normalization factor) = 4 π 2 l + 1 ( l + m ) ! ( l − m ) !
It seems wikipedia’s definition of P l m P_l^m P l m ( − 1 ) m (-1)^m ( − 1 ) m
Associated Legendre polynomials
Spherical harmonics
P 0 0 ( x ) = 1 P_{0}^{0}(x)=1 P 0 0 ( x ) = 1 Y 0 0 ( θ , φ ) = 1 2 1 π Y_{0}^{0}(\theta,\varphi)=\dfrac{1}{2}\sqrt{\dfrac{1}{\pi}} Y 0 0 ( θ , φ ) = 2 1 π 1
P 1 − 1 ( x ) = − 1 2 P 1 1 ( x ) P_{1}^{-1}(x)=-\dfrac{1}{2}P_{1}^{1}(x) P 1 − 1 ( x ) = − 2 1 P 1 1 ( x ) Y 1 − 1 ( θ , φ ) = 1 2 3 2 π sin θ e − i φ Y_{1}^{-1}(\theta,\varphi)={1\over 2}\sqrt{3\over 2\pi} \, \sin\theta \, e^{-i\varphi} Y 1 − 1 ( θ , φ ) = 2 1 2 π 3 sin θ e − i φ
P 1 0 ( x ) = x P_{1}^{0}(x)=x P 1 0 ( x ) = x Y 1 0 ( θ , φ ) = 1 2 3 π cos θ Y_{1}^{0}(\theta,\varphi)={1\over 2}\sqrt{3\over \pi}\, \cos\theta Y 1 0 ( θ , φ ) = 2 1 π 3 cos θ
P 1 1 ( x ) = − ( 1 − x 2 ) 1 / 2 P_{1}^{1}(x)=-(1-x^2)^{1/2} P 1 1 ( x ) = − ( 1 − x 2 ) 1 / 2 Y 1 1 ( θ , φ ) = − 1 2 3 2 π sin θ e i φ Y_{1}^{1}(\theta,\varphi)={-1\over 2}\sqrt{3\over 2\pi}\, \sin\theta\, e^{i\varphi} Y 1 1 ( θ , φ ) = 2 − 1 2 π 3 sin θ e i φ
P 2 − 2 ( x ) = 1 24 P 2 2 ( x ) P_{2}^{-2}(x)=\frac{1}{24}P_{2}^{2}(x) P 2 − 2 ( x ) = 2 4 1 P 2 2 ( x ) Y 2 − 2 ( θ , φ ) = 1 4 15 2 π sin 2 θ e − 2 i φ Y_{2}^{-2}(\theta,\varphi)={1\over 4}\sqrt{15\over 2\pi} \, \sin^{2}\theta \, e^{-2i\varphi} Y 2 − 2 ( θ , φ ) = 4 1 2 π 1 5 sin 2 θ e − 2 i φ
P 2 − 1 ( x ) = − 1 6 P 2 1 ( x ) P_{2}^{-1}(x)=-\frac{1}{6}P_{2}^{1}(x) P 2 − 1 ( x ) = − 6 1 P 2 1 ( x ) Y 2 − 1 ( θ , φ ) = 1 2 15 2 π sin θ cos θ e − i φ Y_{2}^{-1}(\theta,\varphi)={1\over 2}\sqrt{15\over 2\pi}\, \sin\theta\, \cos\theta\, e^{-i\varphi} Y 2 − 1 ( θ , φ ) = 2 1 2 π 1 5 sin θ cos θ e − i φ
P 2 0 ( x ) = 1 2 ( 3 x 2 − 1 ) P_{2}^{0}(x)=\frac{1}{2}(3x^{2}-1) P 2 0 ( x ) = 2 1 ( 3 x 2 − 1 ) Y 2 0 ( θ , φ ) = 1 4 5 π ( 3 cos 2 θ − 1 ) Y_{2}^{0}(\theta,\varphi)={1\over 4}\sqrt{5\over \pi}\, (3\cos^{2}\theta-1) Y 2 0 ( θ , φ ) = 4 1 π 5 ( 3 cos 2 θ − 1 )
P 2 1 ( x ) = − 3 x ( 1 − x 2 ) 1 / 2 P_{2}^{1}(x)=-3x(1-x^2)^{1/2} P 2 1 ( x ) = − 3 x ( 1 − x 2 ) 1 / 2 Y 2 1 ( θ , φ ) = − 1 2 15 2 π sin θ cos θ e i φ Y_{2}^{1}(\theta,\varphi)={-1\over 2}\sqrt{15\over 2\pi}\, \sin\theta\,\cos\theta\, e^{i\varphi} Y 2 1 ( θ , φ ) = 2 − 1 2 π 1 5 sin θ cos θ e i φ
P 2 2 ( x ) = 3 ( 1 − x 2 ) P_{2}^{2}(x)=3(1-x^2) P 2 2 ( x ) = 3 ( 1 − x 2 ) Y 2 2 ( θ , φ ) = 1 4 15 2 π sin 2 θ e 2 i φ Y_{2}^{2}(\theta,\varphi)={1\over 4}\sqrt{15\over 2\pi}\, \sin^{2}\theta \, e^{2i\varphi} Y 2 2 ( θ , φ ) = 4 1 2 π 1 5 sin 2 θ e 2 i φ
Parity :
Y l m ( π − θ , π + ϕ ) = ( − 1 ) l Y l m ( θ , ϕ ) Y^m_l(\pi-\theta,\pi+\phi) = (-1)^lY_l^m(\theta,\phi)
Y l m ( π − θ , π + ϕ ) = ( − 1 ) l Y l m ( θ , ϕ )
This proterties can be checked directly from the definition, no matter it contains ( − 1 ) m (-1)^m ( − 1 ) m
Complex conjugate :
Y l m ∗ ( θ , ϕ ) = ( − 1 ) m Y l − m ( θ , ϕ ) {Y^m_l}^*(\theta,\phi) = (-1)^mY^{-m}_l(\theta,\phi)
Y l m ∗ ( θ , ϕ ) = ( − 1 ) m Y l − m ( θ , ϕ )
Negative m m m : The same as the complex conjugate properties above?
The formual below comes from the central potential 2-body problem. (Hydrogen atom problem) Y = Y ( θ , ϕ ) Y=Y(\theta,\phi) Y = Y ( θ , ϕ )
( ∂ 2 ∂ θ 2 + cot θ ∂ ∂ θ + 1 sin 2 θ ∂ 2 ∂ ϕ 2 ) Y = − l ( l + 1 ) Y \left(\dfrac{\partial^2}{\partial \theta^2} +
\cot\theta\dfrac{\partial}{\partial \theta} +
\dfrac{1}{\sin^2\theta}\dfrac{\partial^2}{\partial \phi^2}
\right)Y = -l(l+1)Y ( ∂ θ 2 ∂ 2 + cot θ ∂ θ ∂ + sin 2 θ 1 ∂ ϕ 2 ∂ 2 ) Y = − l ( l + 1 ) Y
First, we change the variable: x = cos θ x = \cos\theta x = cos θ
∂ ∂ θ = ∂ x ∂ θ ∂ ∂ x = − sin θ ∂ ∂ x \dfrac{\partial}{\partial\theta} = \dfrac{\partial x}{\partial\theta}\dfrac{\partial }{\partial x} = -\sin\theta\dfrac{\partial }{\partial x}
∂ θ ∂ = ∂ θ ∂ x ∂ x ∂ = − sin θ ∂ x ∂
And the second derivative:
∂ 2 ∂ θ 2 = − sin θ ∂ ∂ x ( − sin θ ∂ ∂ x ) = − cos θ ∂ ∂ x + sin 2 θ ∂ 2 ∂ x 2 \begin{aligned}
\dfrac{\partial^2}{\partial\theta^2} & = -\sin\theta\dfrac{\partial }{\partial x}
\left(-\sin\theta\dfrac{\partial }{\partial x}\right)\\
& = -\cos\theta\dfrac{\partial }{\partial x} + \sin^2\theta\dfrac{\partial^2}{\partial x^2}
\end{aligned}
∂ θ 2 ∂ 2 = − sin θ ∂ x ∂ ( − sin θ ∂ x ∂ ) = − cos θ ∂ x ∂ + sin 2 θ ∂ x 2 ∂ 2
Then, the original eigenvalue equation becomes:
( sin 2 θ ∂ 2 ∂ x 2 − 2 cos θ ∂ ∂ x + 1 sin 2 θ ∂ 2 ∂ ϕ 2 ) Y = − l ( l + 1 ) Y ( ( 1 − x 2 ) ∂ 2 ∂ x 2 − 2 x ∂ ∂ x + 1 1 − x 2 ∂ 2 ∂ ϕ 2 ) Y = − l ( l + 1 ) Y \left(\sin^2\theta\dfrac{\partial^2}{\partial x^2}
-2\cos\theta\dfrac{\partial }{\partial x} +
\dfrac{1}{\sin^2\theta}\dfrac{\partial^2}{\partial \phi^2}
\right)Y = -l(l+1)Y\\
\left((1-x^2)\dfrac{\partial^2}{\partial x^2}
-2x\dfrac{\partial }{\partial x} +
\dfrac{1}{1-x^2}\dfrac{\partial^2}{\partial \phi^2}
\right)Y = -l(l+1)Y
( sin 2 θ ∂ x 2 ∂ 2 − 2 cos θ ∂ x ∂ + sin 2 θ 1 ∂ ϕ 2 ∂ 2 ) Y = − l ( l + 1 ) Y ( ( 1 − x 2 ) ∂ x 2 ∂ 2 − 2 x ∂ x ∂ + 1 − x 2 1 ∂ ϕ 2 ∂ 2 ) Y = − l ( l + 1 ) Y
Your can easily seperate Y = P ( x ) Φ ( ϕ ) Y = P(x)\Phi(\phi) Y = P ( x ) Φ ( ϕ ) Φ ′ ′ Φ = − m 2 \dfrac{\Phi''}{\Phi} = -m^2 Φ Φ ′ ′ = − m 2 Φ ( ϕ ) = e ± i m ϕ \Phi(\phi) = e^{\pm im\phi} Φ ( ϕ ) = e ± i m ϕ e − i m ϕ e^{-im\phi} e − i m ϕ P l m P_l^m P l m m m m P ( x ) P(x) P ( x )
[ ( 1 − x 2 ) ∂ 2 ∂ x 2 − 2 x ∂ ∂ x + ( l ( l + 1 ) − m 2 1 − x 2 ) ] P = 0 \left[(1-x^2)\dfrac{\partial^2}{\partial x^2}
-2x\dfrac{\partial }{\partial x} + \left(
l(l+1) - \dfrac{m^2}{1-x^2}\right)
\right]P = 0
[ ( 1 − x 2 ) ∂ x 2 ∂ 2 − 2 x ∂ x ∂ + ( l ( l + 1 ) − 1 − x 2 m 2 ) ] P = 0
And this is the equation appeares at the begining of this chapter. We should get P l m ( x ) P_l^m(x) P l m ( x ) Y ∝ P l m ( x ) e ± i m ϕ Y\propto P_l^m(x)e^{\pm im\phi} Y ∝ P l m ( x ) e ± i m ϕ
x 2 y ′ ′ + x y ′ + ( x 2 − p 2 ) y = 0 \fbox{$x^2y''+xy'+(x^2-p^2)y = 0$}
x 2 y ′ ′ + x y ′ + ( x 2 − p 2 ) y = 0
Or, in the form of eigenvalue problem:
y 2 Y ′ ′ Y + y Y ′ Y + y 2 = p 2 y^2\dfrac{Y''}{Y}+ y\dfrac{Y'}{Y} + y^2 = p^2
y 2 Y Y ′ ′ + y Y Y ′ + y 2 = p 2
J p & N p J_p \& N_p J p & N p To solve the Bessel function y ( x ) y(x) y ( x ) y y y x s x^s x s x 0 x^0 x 0
y = ∑ n = 0 ∞ a n x n + s y = \sum^\infty_{n=0}a_nx^{n+s}
y = n = 0 ∑ ∞ a n x n + s
And finally, we will get two different, sometimes independent solution. One comes from s = p s = p s = p x = − p x = -p x = − p
s = p ⟶ J p ( x ) = ∑ n = 0 ∞ ( − 1 ) n Γ ( n + 1 ) Γ ( n + 1 + p ) ( x 2 ) 2 n + p s = − p ⟶ J − p ( x ) = ∑ n = 0 ∞ ( − 1 ) n Γ ( n + 1 ) Γ ( n + 1 − p ) ( x 2 ) 2 n − p s = p\longrightarrow J_p(x) = \sum^\infty_{n=0}\dfrac{(-1)^n}{\Gamma(n+1)\Gamma(n+1+p)}\left(\dfrac{x}{2}\right)^{2n+p}\\
s = -p\longrightarrow J_{-p}(x) = \sum^\infty_{n=0}\dfrac{(-1)^n}{\Gamma(n+1)\Gamma(n+1-p)}\left(\dfrac{x}{2}\right)^{2n-p}
s = p ⟶ J p ( x ) = n = 0 ∑ ∞ Γ ( n + 1 ) Γ ( n + 1 + p ) ( − 1 ) n ( 2 x ) 2 n + p s = − p ⟶ J − p ( x ) = n = 0 ∑ ∞ Γ ( n + 1 ) Γ ( n + 1 − p ) ( − 1 ) n ( 2 x ) 2 n − p
The relation between J p J_p J p J − p J_{-p} J − p sin \sin sin cos \cos cos J p J_p J p J − p J_{-p} J − p p p p p p p
Althrough J p J_p J p J − p J_{-p} J − p Neumann function or Weber function which is a combination of J p J_p J p J − p J_{-p} J − p J − p J_{-p} J − p
N p ( x ) or Y p ( x ) = cos ( π p ) J p ( x ) − J − p ( x ) sin π p N_p(x) \text{or} Y_p(x)= \dfrac{\cos(\pi p)J_p(x)-J_{-p}(x)}{\sin\pi p}
N p ( x ) or Y p ( x ) = sin π p cos ( π p ) J p ( x ) − J − p ( x )
and general solution of Bessel’s equation is
y = A J p ( x ) + B N p ( x ) y = AJ_p(x)+BN_p(x)
y = A J p ( x ) + B N p ( x )
Picture :
H p ( 1 ) & H p ( 2 ) H_p^{(1)}\& H_p^{(2)} H p ( 1 ) & H p ( 2 ) H p ( 1 ) ( x ) = J p ( x ) + i N p ( x ) H p ( 2 ) ( x ) = J p ( x ) − i N p ( x ) H_p^{(1)}(x) = J_p(x)+iN_p(x)\\
H_p^{(2)}(x) = J_p(x)-iN_p(x)
H p ( 1 ) ( x ) = J p ( x ) + i N p ( x ) H p ( 2 ) ( x ) = J p ( x ) − i N p ( x )
(Compare e ± i x = cos x ± i sin x \mathrm{e}^{\pm ix} = \cos x\pm i\sin x e ± i x = cos x ± i sin x
The differential equation:
y ′ ′ + 1 − 2 a x y ′ + [ ( b c x c − 1 ) 2 + a 2 − p 2 c 2 x 2 ] y = 0 \fbox{$
y'' +\dfrac{1-2a}{x}y' +\left[(bcx^{c-1})^2 + \dfrac{a^2-p^2c^2}{x^2}\right]y =0
$}
y ′ ′ + x 1 − 2 a y ′ + [ ( b c x c − 1 ) 2 + x 2 a 2 − p 2 c 2 ] y = 0
or, in the eigenvalue problem form:
y 2 Y ′ ′ Y + y ( 1 − 2 a ) Y ′ Y + ( b c y c − 1 ) 2 y 2 = p 2 c 2 − a 2 y^2\frac{Y''}{Y} + y(1-2a)\frac{Y'}{Y} + (bcy^{c-1})^2y^2 = p^2c^2-a^2
y 2 Y Y ′ ′ + y ( 1 − 2 a ) Y Y ′ + ( b c y c − 1 ) 2 y 2 = p 2 c 2 − a 2
has the solution:
y = x a [ A J p ( b x c ) + B N p ( b x c ) ] ≡ x a Z p ( b x c ) y = x^a\left[AJ_p(bx^c)+BN_p(bx^c)\right]\equiv x^aZ_p(bx^c)
y = x a [ A J p ( b x c ) + B N p ( b x c ) ] ≡ x a Z p ( b x c )
For a special case, when a = c = 0 a = c =0 a = c = 0
y 2 Y ′ ′ Y + y Y ′ Y + b 2 y 2 = p 2 y^2\dfrac{Y''}{Y} + y\dfrac{Y'}{Y} + b^2y^2 = p^2
y 2 Y Y ′ ′ + y Y Y ′ + b 2 y 2 = p 2
has the solutions J p ( b y ) J_p(by) J p ( b y ) N p ( b y ) N_p(by) N p ( b y )
I p & K p I_p\& K_p I p & K p Start from the “generalbessel function”, if I choose b = i b=i b = i
x 2 y ′ ′ + x y ′ − ( x 2 + p 2 ) y = 0 \fbox{$x^2y''+xy'-(x^2+p^2)y = 0 $}
x 2 y ′ ′ + x y ′ − ( x 2 + p 2 ) y = 0
or in the eigenvalue form:
y 2 Y ′ ′ Y + y Y ′ Y − y 2 = p 2 y^2\dfrac{Y''}{Y}+y\dfrac{Y'}{Y}-y^2 = p^2
y 2 Y Y ′ ′ + y Y Y ′ − y 2 = p 2
has the solution Z p ( i x ) Z_p(ix) Z p ( i x ) J p ( i x ) J_p(ix) J p ( i x ) N p ( i x ) N_p(ix) N p ( i x )
I p ( x ) = i − p J p ( i x ) K p ( x ) = π 2 i p + 1 H p ( 1 ) ( i x ) I_p(x) = i^{-p}J_p(ix)\\
K_p(x) = \dfrac{\pi}{2}i^{p+1}H_p^{(1)}(ix)
I p ( x ) = i − p J p ( i x ) K p ( x ) = 2 π i p + 1 H p ( 1 ) ( i x )
Analogy Bessel/Hyperbolic Bessel with trignometry/hyperbolic trig
Bessel/Hyperbolic Bessel:
x 2 y ′ ′ + x y ′ + x 2 y = p 2 y ⟶ x 2 y ′ ′ + x y ′ − x 2 = p 2 y x^2y''+xy'+x^2y = p^2y\quad\longrightarrow\quad x^2y''+xy'-x^2 = p^2y
x 2 y ′ ′ + x y ′ + x 2 y = p 2 y ⟶ x 2 y ′ ′ + x y ′ − x 2 = p 2 y
Trignometric/Hyperbolic Trig:
y ′ ′ + y = 0 ⟶ y ′ ′ − y = 0 y''+y =0\quad\longrightarrow\quad y''-y=0
y ′ ′ + y = 0 ⟶ y ′ ′ − y = 0
Bessel/Hyperbolic Bessel:
⟶ I p ( x ) = i − p J p ( i x ) , K p ( x ) = π 2 i p + 1 H p ( 1 ) ( i x ) \longrightarrow I_p(x) = i^{-p}J_p(ix),\quad K_p(x) = \dfrac{\pi}{2}i^{p+1}H_p^{(1)}(ix)
⟶ I p ( x ) = i − p J p ( i x ) , K p ( x ) = 2 π i p + 1 H p ( 1 ) ( i x )
Trignometric/Hyperbolic Trig:
⟶ sinh x = − i sin ( i x ) , cosh x = cos ( i x ) \longrightarrow \sinh x = -i\sin(ix),\quad \cosh x = \cos(ix)
⟶ sinh x = − i sin ( i x ) , cosh x = cos ( i x )
pictures :
j n & y n j_n\& y_n j n & y n h n ( 1 ) & h n ( 2 ) h_n^{(1)}\& h_n^{(2)} h n ( 1 ) & h n ( 2 ) When solving the Helmholtz equation in spherical coordinates by separation of variables, the radial equation has the form:
x 2 y ′ ′ + 2 x y ′ + ( x 2 − n ( n + 1 ) ) y = 0 \fbox{$
x^2y''+2xy'+(x^2-n(n+1))y = 0 $}
x 2 y ′ ′ + 2 x y ′ + ( x 2 − n ( n + 1 ) ) y = 0
or, in the form of eigenvalue problem:
y 2 Y ′ ′ Y + 2 y Y ′ Y + y 2 = n ( n + 1 ) y^2\dfrac{Y''}{Y} + 2y\dfrac{Y'}{Y} + y^2 = n(n+1)
y 2 Y Y ′ ′ + 2 y Y Y ′ + y 2 = n ( n + 1 )
The two linearly independent solutions to this equation are called the spherical Bessel functions j n j_n j n y n y_n y n J n J_n J n Y n Y_n Y n
j n ( x ) = π 2 x J n + 1 2 ( x ) y n ( x ) = π 2 x Y n + 1 2 ( x ) = ( − 1 ) n + 1 π 2 x J − n − 1 2 ( x ) j_n(x) = \sqrt{\frac{\pi}{2x}} J_{n+\frac{1}{2}}(x) \\
y_n(x) = \sqrt{\frac{\pi}{2x}} Y_{n+\frac{1}{2}}(x) = (-1)^{n+1} \sqrt{\frac{\pi}{2x}} J_{-n-\frac{1}{2}}(x)
j n ( x ) = 2 x π J n + 2 1 ( x ) y n ( x ) = 2 x π Y n + 2 1 ( x ) = ( − 1 ) n + 1 2 x π J − n − 2 1 ( x )
And we can also define the h n ( 1 , 2 ) h_n^{(1,2)} h n ( 1 , 2 )
h n ( 1 ) = j n ( x ) + i y n ( x ) h n ( 2 ) = j n ( x ) − i y n ( x ) h_n^{(1)} = j_n(x)+iy_n(x)\\
h_n^{(2)} = j_n(x)-iy_n(x)
h n ( 1 ) = j n ( x ) + i y n ( x ) h n ( 2 ) = j n ( x ) − i y n ( x )
Rodrigues formuals :
j n ( x ) = ( − x ) n ( 1 x d d x ) n sin x x y n ( x ) = − ( − x ) n ( 1 x d d x ) n cos x x j_n(x)= (-x)^n \left(\frac{1}{x}\frac{d}{dx}\right)^n\,\frac{\sin x}{x}\\
y_n(x) = -(-x)^n \left(\frac{1}{x}\frac{d}{dx}\right)^n\,\frac{\cos x}{x}
j n ( x ) = ( − x ) n ( x 1 d x d ) n x sin x y n ( x ) = − ( − x ) n ( x 1 d x d ) n x cos x
Notice that if we set p p p p = ( 2 n + 1 ) / 2 = n + 1 / 2 p = (2n+1)/2 = n+1/2 p = ( 2 n + 1 ) / 2 = n + 1 / 2 j n j_n j n y n y_n y n sin x \sin x sin x cos x \cos x cos x x x x
Important notes :
Spherical Bessel function can be expressed by elementary functions !!
j n ( x ) = π 2 x J ( 2 n + 1 ) / 2 ( x ) = x n ( − 1 x d d x ) n ( sin x x ) j_{n}(x)=\sqrt{\frac{\pi}{2 x}} J_{(2 n+1) / 2}(x)=x^{n}\left(-\frac{1}{x} \frac{d}{d x}\right)^{n}\left(\frac{\sin x}{x}\right)
j n ( x ) = 2 x π J ( 2 n + 1 ) / 2 ( x ) = x n ( − x 1 d x d ) n ( x sin x )
y n ( x ) = π 2 x Y ( 2 n + 1 ) / 2 ( x ) = − x n ( − 1 x d d x ) n ( cos x x ) y_{n}(x)=\sqrt{\frac{\pi}{2 x}} Y_{(2 n+1) / 2}(x)=-x^{n}\left(-\frac{1}{x} \frac{d}{d x}\right)^{n}\left(\frac{\cos x}{x}\right)
y n ( x ) = 2 x π Y ( 2 n + 1 ) / 2 ( x ) = − x n ( − x 1 d x d ) n ( x cos x )
j 0 ( x ) = sin x x j 1 ( x ) = sin x x 2 − cos x x \begin{aligned} j_{0}(x) &=\frac{\sin x}{x} \\ j_{1}(x) &=\frac{\sin x}{x^{2}}-\frac{\cos x}{x} \end{aligned}
j 0 ( x ) j 1 ( x ) = x sin x = x 2 sin x − x cos x
Pictures :
A i & B i \mathrm{Ai}\&\mathrm{Bi} A i & B i Airy differential equation is
y ′ ′ − x y = 0 \fbox{$y'' -xy = 0$}
y ′ ′ − x y = 0
In the form of eigenvalue problem:
Y ′ ′ Y − y = 0 \dfrac{Y''}{Y}-y = 0
Y Y ′ ′ − y = 0
It also satisfies the general form of the Bessel differential equation, and the solution is:
x Z 1 / 3 ( 2 3 i x 3 / 2 ) \sqrt{x}Z_{1/3}(\frac{2}{3}ix^{3/2})
x Z 1 / 3 ( 3 2 i x 3 / 2 )
It can be writtern in the combination of J 1 / 3 J_{1/3} J 1 / 3 N 1 / 3 N_{1/3} N 1 / 3 i i i
A i ( x ) = 1 π x 3 K 1 / 3 ( 2 3 x 3 / 2 ) B i ( x ) = x 3 [ I − 1 / 3 ( 2 3 x 3 / 2 ) + I 1 / 3 ( 2 3 x 3 / 2 ) ] \begin{aligned}
\mathrm{Ai}(x) & = \dfrac{1}{\pi}\sqrt{\dfrac{x}{3}}K_{1/3}\left(\dfrac{2}{3}x^{3/2}\right)\\
\mathrm{Bi}(x)& = \sqrt{\dfrac{x}{3}}\left[I_{-1/3}\left(\dfrac{2}{3}x^{3/2}\right) + I_{1/3}\left(\dfrac{2}{3}x^{3/2}\right)\right]
\end{aligned}
A i ( x ) B i ( x ) = π 1 3 x K 1 / 3 ( 3 2 x 3 / 2 ) = 3 x [ I − 1 / 3 ( 3 2 x 3 / 2 ) + I 1 / 3 ( 3 2 x 3 / 2 ) ]
Picture :
Name
Differential euation
Original Bessel
y 2 Y ′ ′ Y + y Y ′ Y + y 2 = p 2 y^2\dfrac{Y''}{Y}+ y\dfrac{Y'}{Y} + y^2 = p^2 y 2 Y Y ′ ′ + y Y Y ′ + y 2 = p 2
General Bessel
y 2 Y ′ ′ Y + y ( 1 − 2 a ) Y ′ Y + ( b c y c − 1 ) 2 y 2 = p 2 c 2 − a 2 y^2\dfrac{Y''}{Y} + y(1-2a)\dfrac{Y'}{Y} + (bcy^{c-1})^2y^2 = p^2c^2-a^2 y 2 Y Y ′ ′ + y ( 1 − 2 a ) Y Y ′ + ( b c y c − 1 ) 2 y 2 = p 2 c 2 − a 2
Hyperbolic Bessel
y 2 Y ′ ′ Y + y Y ′ Y − y 2 = p 2 y^2\dfrac{Y''}{Y}+y\dfrac{Y'}{Y}-y^2 = p^2 y 2 Y Y ′ ′ + y Y Y ′ − y 2 = p 2
Spherical Bessel
y 2 Y ′ ′ Y + 2 y Y ′ Y + y 2 = n ( n + 1 ) y^2\dfrac{Y''}{Y} + 2y\dfrac{Y'}{Y} + y^2 = n(n+1) y 2 Y Y ′ ′ + 2 y Y Y ′ + y 2 = n ( n + 1 )
Kelvin
Y ′ ′ Y + 1 y Y ′ Y = i \dfrac{Y''}{Y} +\dfrac{1}{y}\dfrac{Y'}{Y} = i Y Y ′ ′ + y 1 Y Y ′ = i
Airy
Y ′ ′ Y − y = 0 \dfrac{Y''}{Y}-y = 0 Y Y ′ ′ − y = 0
Lagueere polynomials are solution of the differential equation:
x y ′ ′ + ( 1 − x ) y ′ + n y = 0 \fbox{$
xy''+(1-x)y'+ny = 0 $}
x y ′ ′ + ( 1 − x ) y ′ + n y = 0
or, in the eigenvalue form:
y Y ′ ′ Y + ( 1 − y ) Y ′ Y = − n y\dfrac{Y''}{Y} + (1-y)\dfrac{Y'}{Y} = -n
y Y Y ′ ′ + ( 1 − y ) Y Y ′ = − n
Polynomial means we can expand the solution in a 0 x 0 + a 1 x 1 + a 2 x 2 + ⋯ a_0x^0 + a_1x^1 + a_2x^2+\cdots a 0 x 0 + a 1 x 1 + a 2 x 2 + ⋯
L n ( x ) = 1 − n x + n ( n − 1 ) 2 ! x 2 2 ! n ( n − 1 ) 2 ! x 2 2 ! − n ( n − 1 ) ( n − 2 ) 3 ! x 3 3 ! + ⋯ + ( − 1 ) n x n n ! = ∑ m = 0 n ( − 1 ) m ( n m ) x m m ! \begin{aligned}
L_n(x) & = 1 - nx + \dfrac{n(n-1)}{2!}\dfrac{x^2}{2!}\dfrac{n(n-1)}{2!}\dfrac{x^2}{2!} - \dfrac{n(n-1)(n-2)}{3!}\dfrac{x^3}{3!} +\cdots+\dfrac{(-1)^nx^n}{n!}\\
& = \sum^n_{m=0}(-1)^m{\binom n m}\dfrac{x^m}{m!}
\end{aligned}
L n ( x ) = 1 − n x + 2 ! n ( n − 1 ) 2 ! x 2 2 ! n ( n − 1 ) 2 ! x 2 − 3 ! n ( n − 1 ) ( n − 2 ) 3 ! x 3 + ⋯ + n ! ( − 1 ) n x n = m = 0 ∑ n ( − 1 ) m ( m n ) m ! x m
Warning: some author may omit the 1 / n ! 1/n! 1 / n !
First 3 terms of Lagueere polynomials are:
L 0 ( x ) = 1 L 1 ( x ) = 1 − x L 3 ( x ) = 1 − 2 x + x 2 / 2 \begin{aligned}
L_0(x) & = 1\\
L_1(x) & = 1-x\\
L_3(x) & = 1-2x+x^2/2
\end{aligned}
L 0 ( x ) L 1 ( x ) L 3 ( x ) = 1 = 1 − x = 1 − 2 x + x 2 / 2
Rodrigues formula :
L n ( x ) = 1 n ! e x d n d x n ( x n e − x ) L_n(x) = \dfrac{1}{n!}e^x\dfrac{d^n}{dx^n}(x^ne^{-x})
L n ( x ) = n ! 1 e x d x n d n ( x n e − x )
Orthogonality :
∫ 0 ∞ e − x L n ( x ) L k ( x ) d x = δ n k \int^\infty_0e^{-x}L_n(x)L_k(x)dx = \delta_{nk}
∫ 0 ∞ e − x L n ( x ) L k ( x ) d x = δ n k
Attention that the polynomials are orthogonal on ( 0 , ∞ ) (0,\infty) ( 0 , ∞ ) e − x e^{-x} e − x e x / 2 L n ( x ) e^{x/2}L_n(x) e x / 2 L n ( x )
Generating function :
Φ ( x , h ) = e − x h / ( 1 − h ) 1 − h = ∑ n = 0 ∞ L n ( x ) h n \Phi(x,h) = \dfrac{e^{-xh/(1-h)}}{1-h} = \sum^\infty_{n=0}L_n(x)h^n
Φ ( x , h ) = 1 − h e − x h / ( 1 − h ) = n = 0 ∑ ∞ L n ( x ) h n
Recursion relations :
x y ′ ′ + ( k + 1 − x ) y ′ + n y = 0 \fbox{$ xy''+(k+1-x)y'+ny = 0 $}
x y ′ ′ + ( k + 1 − x ) y ′ + n y = 0
or in the form of the eigenvalue problem:
y Y ′ ′ Y + ( k + 1 − y ) Y ′ Y = − n . y\dfrac{Y''}{Y}+(k+1-y)\dfrac{Y'}{Y} = -n.
y Y Y ′ ′ + ( k + 1 − y ) Y Y ′ = − n .
Actually, the associated Laguerre polynomials are the Derivatives of the Laguerre polynomials . The new polynomials are defined as:
L n k ( x ) = ( − 1 ) k d k d x k L n + k ( x ) L_n^k(x) = (-1)^k\dfrac{d^k}{dx^k}L_{n+k}(x)
L n k ( x ) = ( − 1 ) k d x k d k L n + k ( x )
And all of the properties of the associated Laguerre polynomial could be prooved by using the drivation of Laguerre polynomials.
Warning, again, the formulas and properties here and below will be different if some author omit 1 / n ! 1/n! 1 / n ! L n L_n L n
Rodrigues formula :
L n k ( x ) = x − k e x n ! d n d x n ( x n + k e − x ) L^k_n(x) = \dfrac{x^{-k}e^x}{n!}\dfrac{d^n}{dx^n}(x^{n+k}e^{-x})
L n k ( x ) = n ! x − k e x d x n d n ( x n + k e − x )
Orthogonality :
∫ 0 ∞ x k e − x L n k ( x ) L m k ( x ) d x = δ n m ( n + k ) ! n ! \int^\infty_0x^ke^{-x}L_n^k(x)L_m^k(x)dx = \delta_{nm}\dfrac{(n+k)!}{n!}
∫ 0 ∞ x k e − x L n k ( x ) L m k ( x ) d x = δ n m n ! ( n + k ) !
Note that now the weight function becomes to x k e − x x^ke^{-x} x k e − x
p.s. This orthogonality is not used to normalize the function of hydrogen atom
− ℏ 2 2 m 1 r ∂ 2 ∂ r 2 ( r R ) + [ l ( l + 1 ) ℏ 2 2 m r 2 − e 2 r ] R = E R -\dfrac{\hbar^2}{2m}\dfrac{1}{r}\dfrac{\partial^2}{\partial r^2}\left(rR\right) + \left[\dfrac{l(l+1)\hbar^2}{2mr^2} - \dfrac{e^2}{r}\right]R = ER
− 2 m ℏ 2 r 1 ∂ r 2 ∂ 2 ( r R ) + [ 2 m r 2 l ( l + 1 ) ℏ 2 − r e 2 ] R = E R
STEP 1 , subsititute R ( r ) R(r) R ( r )
R ( r ) = u ( r ) r R(r) = \dfrac{u(r)}{r}
R ( r ) = r u ( r )
Then, the differential equation becomes:
− ℏ 2 2 m ∂ 2 ∂ r 2 u + [ l ( l + 1 ) ℏ 2 2 m r 2 − e 2 r ] u = E u -\dfrac{\hbar^2}{2m}\dfrac{\partial^2}{\partial r^2}u + \left[\dfrac{l(l+1)\hbar^2}{2mr^2} - \dfrac{e^2}{r}\right]u = Eu
− 2 m ℏ 2 ∂ r 2 ∂ 2 u + [ 2 m r 2 l ( l + 1 ) ℏ 2 − r e 2 ] u = E u
STEP 2 is to change some variables to normalize the radius and the energy. ρ ≡ r a 0 \rho\equiv \dfrac{r}{a_0} ρ ≡ a 0 r a 0 a_0 a 0 Bohr radius which is defined as:
a 0 ≡ ℏ 2 m e 2 a_0 \equiv \dfrac{\hbar^2}{me^2}
a 0 ≡ m e 2 ℏ 2
ρ = r a 0 ⟶ − ℏ 2 2 m ∂ 2 a 0 2 ∂ ρ 2 u + [ l ( l + 1 ) ℏ 2 2 m a 0 2 ρ 2 − e 2 a 0 ρ ] u = E u [ − m e 4 2 ℏ 2 ∂ 2 ∂ ρ 2 + l ( l + 1 ) m e 4 2 ℏ 2 ρ 2 − m e 4 ℏ 2 ρ ] u = E u [ ∂ 2 ∂ ρ 2 − l ( l + 1 ) ρ 2 + 2 ρ ] u = − E m e 4 2 ℏ 2 u \rho = \dfrac{r}{a_0}\longrightarrow
-\dfrac{\hbar^2}{2m}\dfrac{\partial^2}{a_0^2\partial \rho^2}u + \left[\dfrac{l(l+1)\hbar^2}{2ma_0^2\rho^2} - \dfrac{e^2}{a_0\rho}\right]u = Eu\\
\left[-\dfrac{me^4}{2\hbar^2}\dfrac{\partial^2}{\partial \rho^2} + \dfrac{l(l+1)me^4}{2\hbar^2\rho^2} - \dfrac{me^4}{\hbar^2\rho}\right]u = Eu\\
\left[\dfrac{\partial^2}{\partial \rho^2} - \dfrac{l(l+1)}{\rho^2} + \dfrac{2}{\rho}\right]u = -\dfrac{E}{\dfrac{me^4}{2\hbar^2}}u
ρ = a 0 r ⟶ − 2 m ℏ 2 a 0 2 ∂ ρ 2 ∂ 2 u + [ 2 m a 0 2 ρ 2 l ( l + 1 ) ℏ 2 − a 0 ρ e 2 ] u = E u [ − 2 ℏ 2 m e 4 ∂ ρ 2 ∂ 2 + 2 ℏ 2 ρ 2 l ( l + 1 ) m e 4 − ℏ 2 ρ m e 4 ] u = E u [ ∂ ρ 2 ∂ 2 − ρ 2 l ( l + 1 ) + ρ 2 ] u = − 2 ℏ 2 m e 4 E u
And we can define the Rydberg energy :
E I ≡ m e 4 2 ℏ 2 E_\mathrm{I} \equiv \dfrac{me^4}{2\hbar^2}
E I ≡ 2 ℏ 2 m e 4
and we have e 2 = 2 a 0 E i , ℏ 2 2 m = a 0 2 E I e^2 = 2a_0E_\mathrm{i}, \dfrac{\hbar^2}{2m} = a_0^2E_\mathrm{I} e 2 = 2 a 0 E i , 2 m ℏ 2 = a 0 2 E I
[ ∂ 2 ∂ ρ 2 − l ( l + 1 ) ρ 2 + 2 ρ ] u = − E E I u [ ∂ 2 ∂ ρ 2 − l ( l + 1 ) ρ 2 + 2 ρ ] u = λ 2 u \left[\dfrac{\partial^2}{\partial \rho^2} - \dfrac{l(l+1)}{\rho^2} + \dfrac{2}{\rho}\right]u = -\dfrac{E}{E_\mathrm{I}}u\\
\left[\dfrac{\partial^2}{\partial \rho^2} - \dfrac{l(l+1)}{\rho^2} + \dfrac{2}{\rho}\right]u = \lambda^2u
[ ∂ ρ 2 ∂ 2 − ρ 2 l ( l + 1 ) + ρ 2 ] u = − E I E u [ ∂ ρ 2 ∂ 2 − ρ 2 l ( l + 1 ) + ρ 2 ] u = λ 2 u
Where, λ \lambda λ λ ≡ − E E I \lambda\equiv\sqrt{-\dfrac{E}{E_\mathrm{I}}} λ ≡ − E I E E < 0 E<0 E < 0
STEP 3 . Not enough yet. Another substitution is needed in order to eliminate the term of λ 2 u \lambda^2u λ 2 u :
u ( ρ ) ≡ y ( ρ ) e − λ ρ u(\rho) \equiv y(\rho)e^{-\lambda\rho}
u ( ρ ) ≡ y ( ρ ) e − λ ρ
and we get:
d u d ρ = d y d ρ e − λ ρ − λ y e − λ ρ d 2 u d ρ 2 = d 2 y d ρ 2 e − λ ρ − 2 λ d y d ρ e − λ ρ + λ 2 y e − λ ρ \dfrac{du}{d\rho} = \dfrac{dy}{d\rho}e^{-\lambda\rho}-\lambda ye^{-\lambda\rho}\\
\dfrac{d^2u}{d\rho^2} = \dfrac{d^2y}{d\rho^2}e^{-\lambda\rho} - 2\lambda\dfrac{dy}{d\rho}e^{-\lambda\rho}+\lambda^2 ye^{-\lambda\rho}
d ρ d u = d ρ d y e − λ ρ − λ y e − λ ρ d ρ 2 d 2 u = d ρ 2 d 2 y e − λ ρ − 2 λ d ρ d y e − λ ρ + λ 2 y e − λ ρ
So the differential equation now becomes:
d 2 y d ρ 2 − 2 λ d y d ρ + [ 2 ρ − l ( l + 1 ) ρ 2 ] y = 0 \dfrac{d^2y}{d\rho^2} - 2\lambda\dfrac{dy}{d\rho} + \left[\dfrac{2}{\rho}-\dfrac{l(l+1)}{\rho^2}\right]y = 0
d ρ 2 d 2 y − 2 λ d ρ d y + [ ρ 2 − ρ 2 l ( l + 1 ) ] y = 0
STEP 4 is to eliminate the term of l ( l + 1 ) ρ 2 y \dfrac{l(l+1)}{\rho^2}y ρ 2 l ( l + 1 ) y . Do the substitution:
y ( ρ ) = ρ s q ( ρ ) = ρ l + 1 q ( ρ ) y(\rho) = \rho^{s}q(\rho) = \rho^{l+1}q(\rho)
y ( ρ ) = ρ s q ( ρ ) = ρ l + 1 q ( ρ )
and we get
y ′ = ( l + 1 ) ρ l q + ρ l + 1 q ′ y ′ ′ = l ( l + 1 ) ρ l − 1 q + 2 ( l + 1 ) ρ l q ′ + ρ l + 1 q ′ ′ y' = (l+1)\rho^lq+\rho^{l+1}q'\\
y'' = l(l+1)\rho^{l-1}q + 2(l+1)\rho^lq'+\rho^{l+1}q''
y ′ = ( l + 1 ) ρ l q + ρ l + 1 q ′ y ′ ′ = l ( l + 1 ) ρ l − 1 q + 2 ( l + 1 ) ρ l q ′ + ρ l + 1 q ′ ′
Actually, s s s s = − l s = -l s = − l
So the differential equation becomes:
ρ q ′ ′ + [ 2 ( l + 1 ) − 2 λ ρ ] q ′ + [ 2 − 2 λ ( l + 1 ) ] q = 0 ρ q ′ ′ q + [ 2 ( l + 1 ) − 2 λ ρ ] q ′ q = − [ 2 − 2 λ ( l + 1 ) ] \rho q'' + [2(l+1)-2\lambda \rho]q' + [2-2\lambda(l+1)]q = 0\\
\rho\dfrac{q''}{q} + [2(l+1)-2\lambda \rho]\dfrac{q'}{q} = -[2-2\lambda(l+1)]
ρ q ′ ′ + [ 2 ( l + 1 ) − 2 λ ρ ] q ′ + [ 2 − 2 λ ( l + 1 ) ] q = 0 ρ q q ′ ′ + [ 2 ( l + 1 ) − 2 λ ρ ] q q ′ = − [ 2 − 2 λ ( l + 1 ) ]
STEP 5 : We are very close to the final answer. We just need to take care the factor − 2 λ ρ q ′ q -2\lambda \rho\dfrac{q'}{q} − 2 λ ρ q q ′ ρ \rho ρ
ξ = 2 λ ρ , ρ = ξ 2 λ \xi = 2\lambda\rho,\quad \rho = \dfrac{\xi}{2\lambda}
ξ = 2 λ ρ , ρ = 2 λ ξ
The differential equation then becomes:
2 λ ξ d 2 q d ξ 2 + ( 2 λ ) [ 2 ( l + 1 ) − ξ ] d q d ξ = − [ 2 − 2 λ ( l + 1 ) ] ξ d 2 q d ξ 2 + [ 2 ( l + 1 ) − ξ ] d q d ξ = − 2 − 2 λ ( l + 1 ) 2 λ ξ d 2 q d ξ 2 + [ ( 2 l + 1 ) + 1 − ξ ] d q d ξ = − [ 1 λ − ( l + 1 ) ] 2\lambda\xi\dfrac{d^2q}{d\xi^2} + (2\lambda)[2(l+1)-\xi]\dfrac{dq}{d\xi} = -[2-2\lambda(l+1)]\\
\xi\dfrac{d^2q}{d\xi^2} + [2(l+1)-\xi]\dfrac{dq}{d\xi} = -\dfrac{2-2\lambda(l+1)}{2\lambda}\\
\xi\dfrac{d^2q}{d\xi^2} + [(2l+1)+1-\xi]\dfrac{dq}{d\xi} = -\left[\dfrac{1}{\lambda}-(l+1)\right]
2 λ ξ d ξ 2 d 2 q + ( 2 λ ) [ 2 ( l + 1 ) − ξ ] d ξ d q = − [ 2 − 2 λ ( l + 1 ) ] ξ d ξ 2 d 2 q + [ 2 ( l + 1 ) − ξ ] d ξ d q = − 2 λ 2 − 2 λ ( l + 1 ) ξ d ξ 2 d 2 q + [ ( 2 l + 1 ) + 1 − ξ ] d ξ d q = − [ λ 1 − ( l + 1 ) ]
Compare with the function of associated Laguerre:
y Y ′ ′ Y + ( k + 1 − x ) Y ′ Y = − n y\dfrac{Y''}{Y}+(k+1-x)\dfrac{Y'}{Y} = -n
y Y Y ′ ′ + ( k + 1 − x ) Y Y ′ = − n
We set
{ k = 2 l + 1 n r = 1 λ − ( l + 1 ) \begin{cases}
k = 2l+1\\
n_r = \dfrac{1}{\lambda}-(l+1)
\end{cases}
⎩ ⎨ ⎧ k = 2 l + 1 n r = λ 1 − ( l + 1 )
Where n r n_r n r λ = 1 n r + l + 1 ≡ 1 n \lambda = \dfrac{1}{n_r+l+1}\equiv\dfrac{1}{n} λ = n r + l + 1 1 ≡ n 1 n = n r + l + 1 n = n_r+l+1 n = n r + l + 1 principal quantum number . We know that n r ≥ 0 n_r\geq 0 n r ≥ 0 n n n n r n_r n r
n = 1 : l = 0 , n r = 0 n = 2 : l = 0 , n r = 1 l = 1 , n r = 0 n = 3 : l = 0 , n r = 2 l = 1 , n r = 1 l = 2 , n r = 0 \begin{aligned}
n = 1 : & l=0, & n_r = 0 \\
n = 2 : & l=0, & n_r = 1 \\
& l=1, & n_r = 0 \\
n = 3 : & l=0, & n_r = 2 \\
& l=1, & n_r = 1 \\
& l=2, & n_r = 0
\end{aligned}
n = 1 : n = 2 : n = 3 : l = 0 , l = 0 , l = 1 , l = 0 , l = 1 , l = 2 , n r = 0 n r = 1 n r = 0 n r = 2 n r = 1 n r = 0
So that:
n r = n − l − 1 n_r = n-l-1
n r = n − l − 1
And the solution for the q ( ξ ) q(\xi) q ( ξ )
q ( ξ ) = L n r k ( ξ ) = L n − l − 1 2 l + 1 = q n l ( ξ ) q(\xi) = L^k_{n_r}(\xi) = L^{2l+1}_{n-l-1} = q_{nl}(\xi)
q ( ξ ) = L n r k ( ξ ) = L n − l − 1 2 l + 1 = q n l ( ξ )
Finally , let’s go over the whole transmission during the derivation:
R ( r ) = u ( r ) r = y ( ρ ) e − λ ρ r = y ( ρ ) e − λ r / a 0 r = ρ l + 1 q ( ρ ) e − λ r / a 0 r = ( r / a 0 ) l + 1 q ( ρ ) e − λ r / a 0 r = ( r / a 0 ) l + 1 q ( ξ ) e − λ r / a 0 r = ( r / a 0 ) l + 1 e − λ r / a 0 r q ( ξ = 2 λ ρ = 2 λ r a 0 ) = ( r / a 0 ) l + 1 e − λ r / a 0 r q ( 2 λ r a 0 ) R n l ( r ) = ( r / a 0 ) l + 1 e − r / n a 0 r q n l ( 2 r n a 0 ) = ( r / a 0 ) l + 1 e − r / n a 0 r L n − l − 1 2 l + 1 ( 2 r n a 0 ) \begin{aligned}
R(r) & = \dfrac{u(r)}{r}\\
& = \dfrac{y(\rho)e^{-\lambda\rho}}{r}\\
& = \dfrac{y\left(\rho\right)e^{-\lambda r/{a_0}}}{r}\\
& = \dfrac{\rho^{l+1}q(\rho)e^{-\lambda r/{a_0}}}{r}\\
& = \dfrac{(r/a_0)^{l+1}q(\rho)e^{-\lambda r/{a_0}}}{r}\\
& = \dfrac{(r/a_0)^{l+1}q(\xi)e^{-\lambda r/{a_0}}}{r}\\
& = \dfrac{(r/a_0)^{l+1}e^{-\lambda r/{a_0}}}{r}q\left(\xi = 2\lambda\rho = \frac{2\lambda r}{a_0}\right)\\
& = \dfrac{(r/a_0)^{l+1}e^{-\lambda r/{a_0}}}{r}q\left(\frac{2\lambda r}{a_0}\right)\\
R_{nl}(r) & = \dfrac{(r/a_0)^{l+1}e^{-r/n{a_0}}}{r}q_{nl}\left(\frac{2r}{na_0}\right)\\
& = \dfrac{(r/a_0)^{l+1}e^{-r/n{a_0}}}{r}L^{2l+1}_{n-l-1}\left(\frac{2r}{na_0}\right)\\
\end{aligned}
R ( r ) R n l ( r ) = r u ( r ) = r y ( ρ ) e − λ ρ = r y ( ρ ) e − λ r / a 0 = r ρ l + 1 q ( ρ ) e − λ r / a 0 = r ( r / a 0 ) l + 1 q ( ρ ) e − λ r / a 0 = r ( r / a 0 ) l + 1 q ( ξ ) e − λ r / a 0 = r ( r / a 0 ) l + 1 e − λ r / a 0 q ( ξ = 2 λ ρ = a 0 2 λ r ) = r ( r / a 0 ) l + 1 e − λ r / a 0 q ( a 0 2 λ r ) = r ( r / a 0 ) l + 1 e − r / n a 0 q n l ( n a 0 2 r ) = r ( r / a 0 ) l + 1 e − r / n a 0 L n − l − 1 2 l + 1 ( n a 0 2 r )
R n l ( r ) = r l a 0 l + 1 e − r / n a 0 L n − l − 1 2 l + 1 ( 2 r n a 0 ) \fbox{$R_{nl}(r) = \dfrac{r^l}{a_0^{l+1}}e^{-r/n{a_0}}L^{2l+1}_{n-l-1}\left(\frac{2r}{na_0}\right)$}
R n l ( r ) = a 0 l + 1 r l e − r / n a 0 L n − l − 1 2 l + 1 ( n a 0 2 r )
Attention. the normalization of the solution is not the orthogonality above. We should use
∫ 0 ∞ x k + 1 e − x [ L n k ( x ) ] 2 d x = ( 2 n + k + 1 ) ( n + k ) ! n ! \int^\infty_0x^{k+1}e^{-x}[L^k_n(x)]^2dx = (2n+k+1)\dfrac{(n+k)!}{n!}
∫ 0 ∞ x k + 1 e − x [ L n k ( x ) ] 2 d x = ( 2 n + k + 1 ) n ! ( n + k ) !
x y ′ ′ + ( c − x ) y − a y = 0 \fbox{$
xy''+(c-x)y-ay = 0 $}
x y ′ ′ + ( c − x ) y − a y = 0
or the eigenvalue problem form:
y Y ′ ′ Y + ( c − y ) Y ′ Y = a y\dfrac{Y''}{Y} + (c-y)\dfrac{Y'}{Y} = a
y Y Y ′ ′ + ( c − y ) Y Y ′ = a
F ( a , c ; x ) & G ( a , c ; x ) F(a,c;x)\& G(a,c;x) F ( a , c ; x ) & G ( a , c ; x ) The solution which is regular at the origin is called the confluent hypergeometric function and denoted as F ( a , c ; x ) F(a, c; x) F ( a , c ; x ) 1 F 1 ( a , c ; x ) {}_1F_1(a, c; x) 1 F 1 ( a , c ; x ) Gauss hypergeometric function .
Name
differential equation
Legendre
( 1 − y 2 ) Y ′ ′ Y − 2 y Y ′ Y = − l ( l + 1 ) (1-y^2)\dfrac{Y''}{Y}-2y\dfrac{Y'}{Y} = -l(l+1) ( 1 − y 2 ) Y Y ′ ′ − 2 y Y Y ′ = − l ( l + 1 )
Associated Legendre
( 1 − y 2 ) Y ′ ′ Y − 2 y Y ′ Y − m 2 1 − y 2 = − l ( l + 1 ) (1-y^2)\dfrac{Y''}{Y}-2y\dfrac{Y'}{Y} - \dfrac{m^2}{1-y^2} = -l(l+1) ( 1 − y 2 ) Y Y ′ ′ − 2 y Y Y ′ − 1 − y 2 m 2 = − l ( l + 1 )
Bessel
y 2 Y ′ ′ Y + y Y ′ Y + y 2 = p 2 y^2\dfrac{Y''}{Y}+ y\dfrac{Y'}{Y} + y^2 = p^2 y 2 Y Y ′ ′ + y Y Y ′ + y 2 = p 2
Hermite
Y ′ ′ Y − 2 y Y ′ Y = − 2 n \dfrac{Y''}{Y} -2y\dfrac{Y'}{Y} = -2n Y Y ′ ′ − 2 y Y Y ′ = − 2 n
Laguerre
y Y ′ ′ Y + ( 1 − y ) Y ′ Y = − n y\dfrac{Y''}{Y}+(1-y)\dfrac{Y'}{Y} = -n y Y Y ′ ′ + ( 1 − y ) Y Y ′ = − n
Associated Laguerre
y Y ′ ′ Y + ( k + 1 − y ) Y ′ Y = − n y\dfrac{Y''}{Y}+(k+1-y)\dfrac{Y'}{Y} = -n y Y Y ′ ′ + ( k + 1 − y ) Y Y ′ = − n
Confluent hypergeometric function
y Y ′ ′ Y + ( c − y ) Y ′ Y = a y\dfrac{Y''}{Y} + (c-y)\dfrac{Y'}{Y} = a y Y Y ′ ′ + ( c − y ) Y Y ′ = a